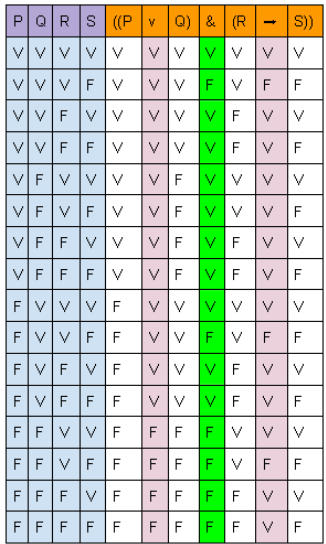
Una tabla de verdad es una herramienta que se utiliza en lógica para analizar todas las posibles combinaciones de valores de verdad de una proposición o conjunto de proposiciones. Tiene como propósito mostrar de manera clara cómo se determinan los valores de verdad de una expresión lógica dependiendo de los valores de las proposiciones que la componen.
1.- Situaciones a evaluar
El primer paso para hacer nuestra tabla de verdad es definir los valores de verdad posibles que tendremos, para definir esto, primero debemos de saber cuantas proposiciones tenemos. Por ejemplo, en la fórmula lógica ((P v (Q & R)) v Q), aunque existen 4 letras dentro de la fórmula, realmente solo hay 3, puesto que no consideraremos para esto repeticiones.
Empecemos por lo más intuitivo, si tuviéramos una sola proposición en nuestra fórmula, “(P)”, por dar un ejemplo. Supongamos que (P), se traduce al lenguaje natural como “Está lloviendo”, bajo esta premisa, ¿Cuáles son los posibles valores de verdad de (P)?, no es necesario pensar en tecnicismos, responder a si está lloviendo es únicamente verdadero o falso, por lo que si quisiéramos hacerle una tabla de verdad a la fórmula (P), únicamente tendríamos 2 escenarios.
Ahora si empezamos con la tabla, para empezar, nuestras proposiciones (en este primer escenario solo es una), y en las filas hacia abajo todas nuestras posibles situaciones de verdad, en este caso, solo V y F.
¿Qué pasa cuándo hay más proposiciones? agregaremos más situaciones. Supongamos que tenemos ahora la oración “Está lloviendo y hace frío”, lo que en lenguaje lógico se traducirá cómo (P & Q), ahora tenemos 2 proposiciones, y (Q) también puede ser o verdadera o falsa, entonces nuestras posibles situaciones siguen siendo 2?. No, la respuesta es un “no”, si Q estuviera sola, no hubiera otra posible proposición, si sería la misma situación que hemos analizado anteriormente, en cambio, en esta fórmula, tenemos 2 proposiciones, P y Q, y para poder definir cuantas situaciones tendremos para nuestra fórmula, tendremos que hacer una pequeña cuenta matemática, no te preocupes, no es difícil.
Cuando hay 2 o más proposiciones, para definir cuántos valores de verdad tiene nuestra tabla, hay que agarrar cada una de nuestras proposiciones, y suponer que cada una vale “2”, y multiplicaremos todas nuestras proposiciones, de modo que, si tienes 2 proposiciones, obtenemos que 2*2=4, 4 van a ser las posibles situaciones que tendrá nuestra tabla de verdad. Suponiendo que tuvieras 3 proposiciones, (P & (Q v R)), entonces tenemos que 2*2*2=8, si tuviéramos 4 sería 2*2*2*2=16, si tuviéramos 5 sería 2*2*2*2*2=32… y así hasta X proposiciones diferentes que tenga tu fórmula.
Por ahora por cuestiones prácticas nos quedaremos únicamente con 3 proposiciones, tendremos ocho situaciones de verdad. ¿Por qué si cada proposición solo puede ser verdadera o falsa, tenemos ocho situaciones y no solo 2 que corresponden a verdadero o falso?, la respuesta es sencilla, únicamente serían 2 situaciones si todas las proposiciones siempre tuvieran el mismo valor de verdad, por ejemplo, que en todas las situaciones, o las 3 proposiciones son verdaderas, o las 3 son falsas, en cambio, esto no es el caso, puesto que se pueden hacer muchas combinaciones, hay una situación donde la primera premisa es verdadera, la segunda es falsa y la tercera es falsa; o una situación donde la primera es falsa, la segunda es verdadera y la tercera es falsa.
Es por esto, que evaluaremos ocho situaciones, porque son ocho posibles combinaciones las que se harán teniendo 3 proposiciones. La tabla tendrá 3 columnas (una por cada proposición) y 8 filas (una para cada combinación posible).
Como tip para rellenar tu tabla, para la última proposición, sus valores de verdad irán intercalados de 1 en 1 (V,F,V,F,V,F,V,F…) así hasta rellenar todas las filas, tu penúltima proposición harás lo mismo, pero intercalando de 2 en 2, (V,V,F,F,V,V,F,F), la siguiente de 4 en 4, y así duplicando la secuencia hasta llegar a tu primera proposición y por cada columna que haya.
Para 3 proposiciones, R será la que tenga sus valores intercalados 1 en 1, Q de 2 en 2, y P de 4 en 4

2.- Definir conectivo principal
Una vez hemos definido nuestros posibles valores de verdad, tenemos que dedicar nuevas columnas para nuestra fórmula lógica, yo en lo personal recomiendo añadir una por cada proposición y símbolo que aparezca en la oración, aunque esto puede variar según las exigencias de tu profesor, o que tanta práctica vayas acumulando. Para esta sección usaré la fórmula (P & (Q v P)).
Para definir nuestro conectivo principal, hay que pensar en cómo está estructurada la fórmula, como si se tratara de “cajas”. El conectivo principal es el que conecta la caja más grande de la fórmula. Si la fórmula tiene paréntesis, ellos agrupan “sub fórmulas” más pequeñas. Los conectivos que están dentro de los paréntesis son internos, así que no serán el principal. Mira qué otros símbolos están fuera de estos paréntesis, porque ahí estará el conectivo principal.
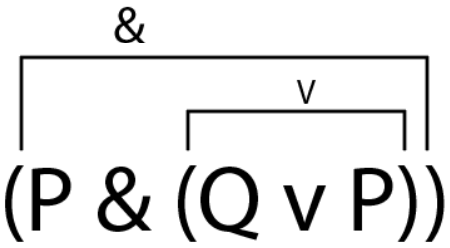
En este caso, nuestro conectivo principal es “&”, ya que se ubica en la caja más grande de toda la fórmula, mientras que “v” se ubica en una sub formula. Esto igual se ve afectado con los símbolos de negación (¬), así que uno de estos también puede ser un conectivo principal
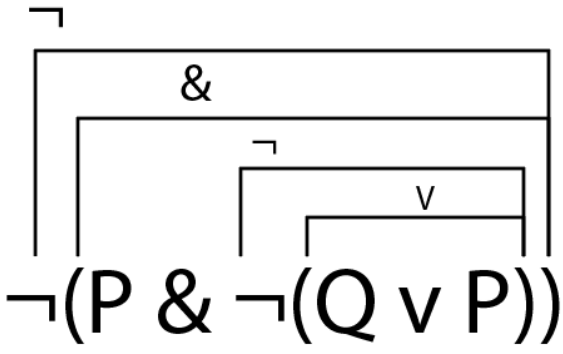
Es importante definir cuál es nuestro conectivo principal, ya que con esto, podremos definir en qué orden hacer nuestra tabla de verdad.
3.- TABLAS:D
Para empezar nuestra tabla, debemos iniciar siempre desde los paréntesis que estén más al interior de nuestra fórmula, en fórmulas de gran tamaño, por ejemplo (((P v Q) v (Q v P)) & ((P v Q) v (Q v P))), donde existen varias sub formulas que comparten el mismo nivel jerárquico, es indistinto por cual de todas estas empecemos, mientras hagamos las demás sub formulas que nos permitan resolver sus conectivos superiores (los que están en las cajas más grandes).
Regresando a la fórmula del punto anterior, (P & (Q v P)), aquí, (Q v P) son la sub formula más pequeña, por lo que debe de ser la primera en resolverse. Para empezar, se recomienda transcribir los valores de verdad de cada posible situación en su respectiva proposición de la fórmula, este paso se puede omitir y pasar a la evaluación de su conectivo, en cambio, esto no lo recomiendo si apenas estás aprendiendo a hacer tablas de verdad.

Una vez hemos transcrito los valores de verdad de cada proposición, únicamente nos queda definir si nuestro conectivo es verdadero o falso, para este paso es importante conocer ya los valores de verdad que puede obtener la interacción de 2 proposiciones con distintos símbolos lógicos, por lo que se recomienda leer nuestras publicaciones previas sobre conectivos lógicos.
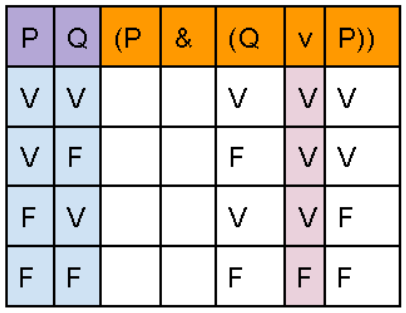
Ya hemos logrado hacer la primera parte de nuestra tabla, el siguiente paso será repetir el mismo proceso con la cantidad de sub formulas que hayan disponibles en nuestra fórmula, así hasta llegar al conectivo principal. Primero hacemos nuestra transcripción.
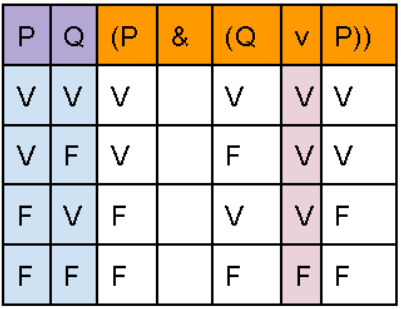
Y ahora debemos de evaluar los valores de verdad de la conjunción, en cambio, este no se debe de evaluar con el símbolo que tiene inmediatamente después, sino que, debe de evaluarse con el valor de verdad de la sub formula que ya previamente resolvimos, en este caso, con el valor de verdad de la disyunción de la sub formula (Q v P), el cual es el valor general de dicha caja.
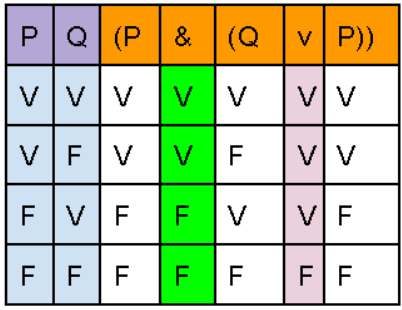
Así, los resultados que obtenemos serán los posibles valores de verdad de nuestra fórmula, y finalmente, conseguimos completar la tabla de verdad. Un proceso un tanto laborioso, pero que al final se va haciendo automáticamente.
Ejemplo de tablas más amplias: